Understanding JavaScript Functions

Published:Nov 8, 2017

Imagine you live in an village without tap water. To get water, you need to take a empty bucket, head to the well in the middle of the village, draw water from the well and head back home.

You need to draw water from this well multiple times a day. It’s a hassle to say “I’m going to take an empty bucket, go to the well, draw water and bring back home” every time you explain what you’re doing.

To shorten it, you can say you’re going to “draw water”.

And my friend, you’ve created a function.

Declaring functions

A function is a block of code that executes tasks in a specific order, like take empty bucket, go to well, draw water, head back home.

It can be defined with the following syntax:

function functionName(parameters) {
  // Do stuff here
}

function is a keyword that tells JavaScript you’re defining a function.

functionName is the name of the function. In the example given above, the function name could be drawWater.

The name of the function can be anything, as long as it follows the same rules as declaring variables. In other words, it needs to follow these rules:

It must be one word
It must consist only of letters, numbers or underscores (0-9, a-z, A-Z, _).
It cannot begin with a number.
It cannot be any of these reserved keywords

parameters is optional. It is a comma-separated list of variables you wish to declare for your function. They can be assigned values when you use the function.

Using functions

Once you declared your function, you can use (or invoke, or call, or execute) it by writing the name of the function, followed by parenthesis ().

Here’s an example where a sayHello function is declared and used.

// Declaring a function
function sayHello() {
  console.log('Hello world!')
}

// using a function
sayHello()

The indentation

Code within a block (anything within curly braces {}) should be indented to the right. This is an important practice that helps you make code easier to read. It allows you to tell at a glance that console.log('Hello world') is part of sayHello.

function sayHello() {
  // This console.log statement is a part of sayHello
  console.log('Hello world!')
}

You can choose to indent with 2 spaces or with a tab key. Some people prefer spaces, others prefer tab. Both are fine, as long as you keep it consistent.

Parameters

Most functions take in parameters. It is a comma-separated list of variables you wish to declare for your function.

You can have any number of parameters.

function functionName(param1, param2, param3) {
  // Do stuff here
}

To assign values to your parameters, you pass in values (called arguments) by writing them as comma-separated values in the parenthesis

The first argument would be assigned to the first parameter, the second argument to the second parameter and so on.

functionName('arg1', 'arg2')

Let’s make it clearer with an example.

Let’s say you wish to write a function called sayName that logs the firstName and lastName of a person. The function looks like this:

function sayName(firstName, lastName) {
  console.log('firstName is ' + firstName)
  console.log('lastName is ' + lastName)
}

Zell is my first name, Liew is my last name. To get the function to work correctly, I pass my Zell, as the first argument, and Liew as the second argument:

sayName('Zell', 'Liew')
// firstName is Zell
// lastName is Liew

If you declared an parameter, but did not pass a argument to it, your parameter would be undefined.

sayName()
// firstName is undefined
// lastName is undefined

The return statement

Functions can have a return statement that consists of the return keyword and a value:

function functionName() {
  return 'some-value'
}

When JavaScript sees this return statement, it stops executing the rest of the function and “returns” (passes the value back to the function call).

function get2() {
  return 2
  console.log('blah') // This is not executed
}

const results = get2()
console.log(results) // 2
// Note: You would not see 'blah' in the console

If the return value is an expression, JavaScript evaluates the expression before returning the value.

Remember, Javascript can only pass around primitives (like String, Numbers, Booleans) and objects (like functions, arrays and objects) as values. Anything else needs to be evaluated.

Flow of a function

Functions can be hard for beginners to understand. To make sure you understand functions completely, let’s go through what happens when you declare and use a function again. This time, we’ll take things one step at a time.

Here’s the code we’re dissecting:

function add2(num) {
  return num + 2
}

const number = add2(8)
console.log(number) // 10

First of all, you need to declare a function before you can use it. In the first line, JavaScript sees the function keyword and knows the function is called add2.

It skips over the code in the function at this point because the function is not used yet.

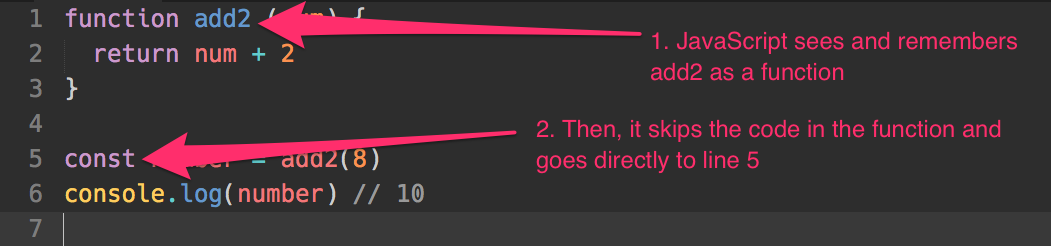
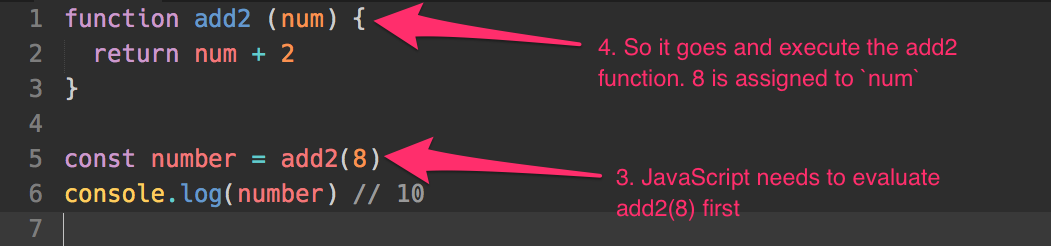
Next, JavaScript sees you’re declaring a variable called number, and assigning it as the result of add2(8).

Since the right hand side (RHS) is a function call (an expression), JavaScript needs to evaluate the value of add2(8) before it can assign it to the number variable. Here, it sets the parameter num to 8, since you passed in 8 as the argument when you call add2(8).

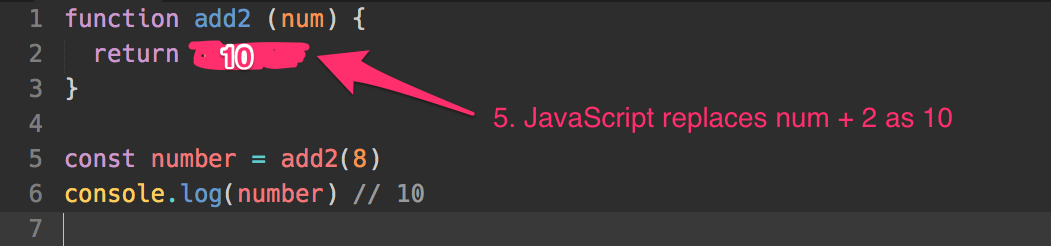
In the add2 function, JavaScript sees a return statement that says num + 2. This is an expression, so it needs to evaluate it before moving on. Since num is 8, num + 2 must be 10.

Once num + 2 is evaluated, JavaScript returns the value to the function call. It replaces the function call with the returned value. So, add2(8) becomes 10.

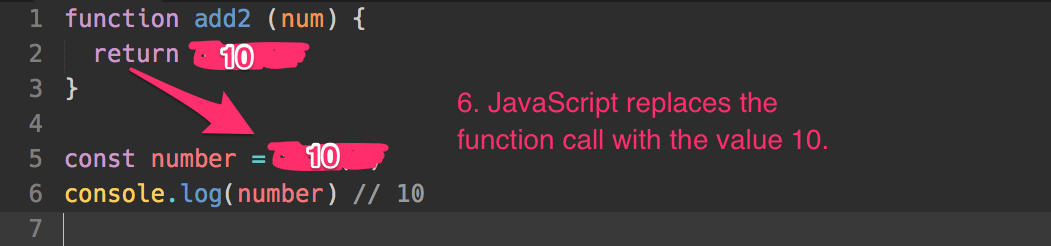
JavaScript replaces add2(8) with the result, 10

Finally, once the RHS is evaluated, JavaScript creates the variable, number and assigns the value 10 to it.

That’s how you read the flow of a function.

Hoisting

When functions are declared with a function declaration (what you learned above), they are hoisted to the top of your scope. This means the following two sets of code are exactly the same.

function sayHello() {
  console.log('Hello world!')
}
sayHello()

// This is automatically converted to the above code
sayHello()
function sayHello() {
  console.log('Hello world!')
}

Function hoisting gets confusing because JavaScript changes the order of your code. I highly recommend you declare your functions before you use them. Don’t rely on hoisting.

Declaring functions with function expressions

A second way to declare functions is with a function expression. Here, you declare a variable, then assign a function without a name (an anonymous function) to it.

const sayHello = function () {
  console.log('This is declared with a function expression!')
}

Note that functions declared with function expressions are not automatically hoisted to the top of your scope.

sayHello() // Error, sayHello is not defined
const sayHello = function () {
  console.log('this is a function!')
}

At this point, you may wonder if function expressions are important. That’s a common question to have. Why would you use function expressions if you can declare functions with the function declaration syntax?

They are important. You’ll learn why when you learn to declare object methods and arrow functions.

Wrapping up

A function is a block of code that executes tasks in a specific order, like take empty bucket, go to well, draw water, head back home.

You call functions by adding a () to the end of the function name. When you do so, you can add additional values as arguments to the function.

Each function can have a return statement that “returns” a value to the function call.

As much as possible, don’t rely on hoisting when you write functions. Always declare them upfront before you use them.

This article is a sample lesson from Learn JavaScript – a course that helps you learn JavaScript to real, practical components from scratch. You’ll love Learn JavaScript if you found this article helpful. If you loved this article, I invite you to find out more about Learn JavaScript.